
The right angle is 90°, leaving the remaining angle to be 30°.


After dividing by 3, the angle α + δ must be 60°. The proof of this fact is simple and follows on from the fact that if α, α + δ, α + 2 δ are the angles in the progression then the sum of the angles 3 α + 3 δ = 180°. The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression. The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem. Then ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1. The geometric proof is:ĭraw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC. The proof of this fact is clear using trigonometry. This is a triangle whose three angles are in the ratio 1 : 2 : 3 and respectively measure 30° ( π / 6), 60° ( π / 3), and 90° ( π / 2). The side lengths of a 30°–60°–90° triangle Special triangles are used to aid in calculating common trigonometric functions, as below: This approach may be used to rapidly reproduce the values of trigonometric functions for the angles 30°, 45°, and 60°. The side lengths are generally deduced from the basis of the unit circle or other geometric methods. The angles of these triangles are such that the larger (right) angle, which is 90 degrees or π / 2 radians, is equal to the sum of the other two angles.

"Angle-based" special right triangles are specified by the relationships of the angles of which the triangle is composed. I will be giving my students part of tomorrow’s class to finish the activity.Special angle-based triangles inscribed in a unit circle are handy for visualizing and remembering trigonometric functions of multiples of 30 and 45 degrees. Students should demonstrate a variety of Mathematical Practices as the work through the activity today. More specifically, I want my students to review and retain the ratios for 45-45-90 and 30-60-90 right triangles. Their focus today should not be the fact that side length ratios hold in similar triangles. It will help students to build on this prior knowledge. So before my students dive into the activity, I am going to have a student quickly summarize what we did yesterday. This activity builds on the concepts of similar right triangles that students studied yesterday. They then analyze a variety of side length ratios to make a conclusion that is true for all special right triangles of that size. For example, students derive the 45-45-90 special right triangle by cutting a rectangle in half diagonally. I like how this activity guides students into creating the special triangles based on facts they already know. Students will be working through Student Worksheet - Special_Right_Triangles.įor some teacher hints and tips from TI, see Teacher Resource - Special_Right_Triangles. The original lesson can be accessed here. Since this is a review lesson, students will be working through the Special Right Triangles TI-Nspire activity from the Texas Instruments website individually.
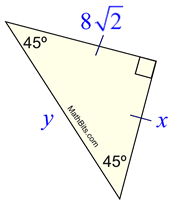
My goal for today is to provide my students with an opportunity to review the properties of 30-60-90 and isosceles right triangles. I plan to have the files already on the calculators before the start of class. Today's lesson requires students to work through a.


 0 kommentar(er)
0 kommentar(er)
